Assignment
📌 Overview
A brief description of the assignment.
Questions
Q3
| Current State (Code) | Current State (Q1Q0) | Inputs | Next State (D1D0) | Next State (Code) | Output (Z) |
|---|---|---|---|---|---|
| Q1 | Q0 | A | B | D1 | |
| S0 | 0 | 0 | 0 | 0 | 0 |
| S0 | 0 | 0 | 0 | 1 | 0 |
| S0 | 0 | 0 | 1 | 0 | 0 |
| S0 | 0 | 0 | 1 | 1 | 0 |
| S1 | 0 | 1 | 0 | 0 | 0 |
| S1 | 0 | 1 | 0 | 1 | 1 |
| S1 | 0 | 1 | 1 | 0 | 1 |
| S1 | 0 | 1 | 1 | 1 | 1 |
| S2 | 1 | 0 | 0 | 0 | 1 |
| S2 | 1 | 0 | 0 | 1 | 1 |
| S2 | 1 | 0 | 1 | 0 | 1 |
| S2 | 1 | 0 | 1 | 1 | 1 |
| S3 | 1 | 1 | 0 | 0 | 1 |
| S3 | 1 | 1 | 0 | 1 | 1 |
| S3 | 1 | 1 | 1 | 0 | 1 |
| S3 | 1 | 1 | 1 | 1 | 1 |
Q4
K-map for D1:
The map is populated with the values from the ‘D1’ column of the state table.
| Q1Q0 \ AB | 00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 0 | 0 |
| 01 | 0 | 1 | 1 | 1 |
| 11 | 1 | 1 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 |
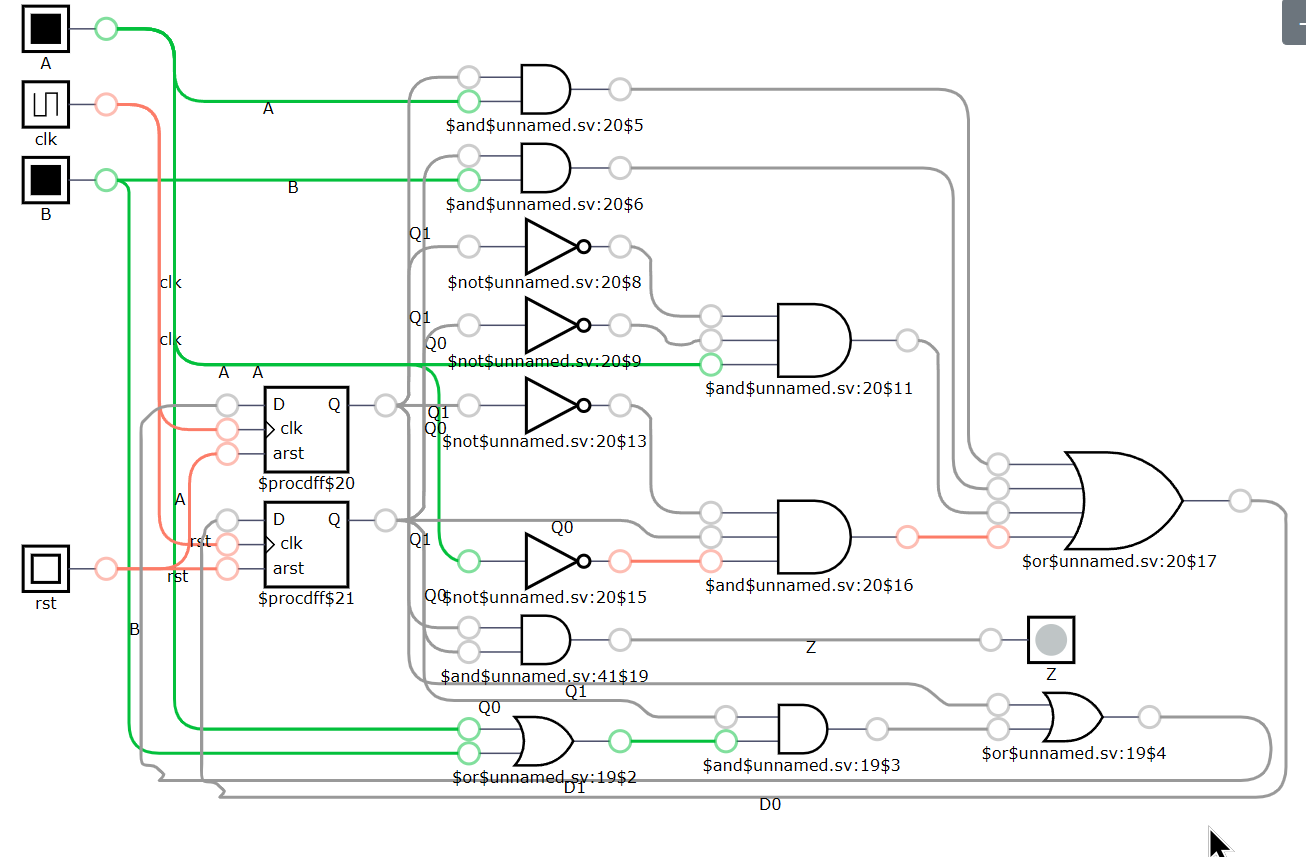
| D1 = Q1 + Q0·A + Q0·B | ||||
| D1 = Q1 + Q0·(A + B) |
K-map for D0:
The map is populated with the values from the ‘D0’ column of the state table.
| Q1Q0 \ AB | 00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 1 | 1 |
| 01 | 1 | 1 | 1 | 0 |
| 11 | 1 | 1 | 1 | 1 |
| 10 | 0 | 1 | 1 | 1 |
| D0 = Q1·A + Q0·B + Q1’·Q0’·A + Q1’·Q0·A’ |
K-map for Output Z:
The output Z is a Moore output, meaning it only depends on the current state (Q1, Q0). Z is 1 only for state S3 (Q1Q0 = 11).
| Q1Q0 \ AB | 00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 |
| 11 | 1 | 1 | 1 | 1 |
| 10 | 0 | 0 | 0 | 0 |
| Z = Q1·Q0 | ||||
 |
stim = Z+W