Assignment
📌 Overview
A brief description of the assignment.
✏️ Exercises
1.1
1B.1
Z=(XY)’=((A(AB)’)‘(B(AB)’)’)’
X=(AW)’=(A(AB)’)’
Y=(BW)’=(B(AB)’)’
W=(AB)’
Let’s assume there was a typo in the original problem and it was ((A + (AB)’)‘(B + (AB)’)’)‘.
Let X = (AB)‘. The expression is ((A + X)‘(B + X)’)‘.
By De Morgan’s Law: (A + X)” + (B + X)”.
By Double Negation: A + X + B + X.
By Idempotent Law (X + X = X): A + B + X.
Substituting X = (AB)’: A + B + (AB)‘.
By De Morgan’s Law: A + B + A’ + B’.
Since A + A’ = 1 and B + B’ = 1, the expression becomes 1 + 1 which is 1.
1B.2 See pdf
1C
| A | A | ||||||
|---|---|---|---|---|---|---|---|
| CD\AB | 00 | 01 | 10 | 11 | |||
| 00 | 0 | 4 | 8 | 12 | |||
| 01 | 1 | 5🔴 | 9 | 13🔴 | D | ||
| C | 10 | 2 | 6 | 10 | 14 | ||
| C | 11 | 3🔴 | 7🔴 | 11🔴 | 15 | D | |
| B | B | ||||||
| X = BC’D+B’CD+A’CD=D(BC’+B’C+A’C) = D(B^C+A’C) |
| A | A | |||||
|---|---|---|---|---|---|---|
| CD\AB | 00 | 01 | 11 | 10 | ||
| 00 | 0 | 4 | 12 | 8 | ||
| 01 | 1 | 5🔴 | 13🔴 | 9 | D | |
| C | 11 | 3🔴 | 7🔴 | 15 | 11🔴 | D |
| C | 10 | 2 | 6 | 14 | 10 | |
| B | B |
.i 4
.o 1
.ilb a b c d
.ob x
.p 16
0000 0
0001 0
0010 0
0011 1
0100 0
0101 1
0110 0
0111 1
1000 0
1001 0
1010 0
1011 1
1100 0
1101 1
1110 0
1111 0
.e
→
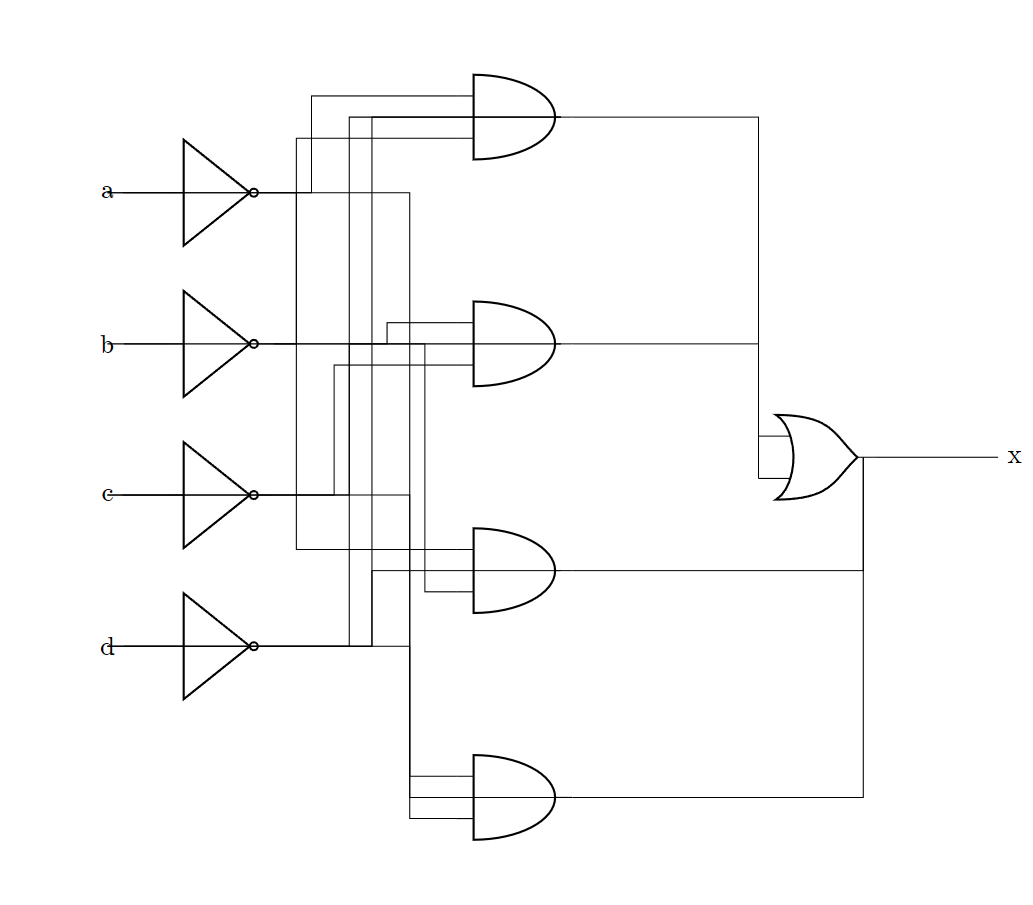
x = (!a&c&d) | (b&!c&d) | (!b&c&d);
1A
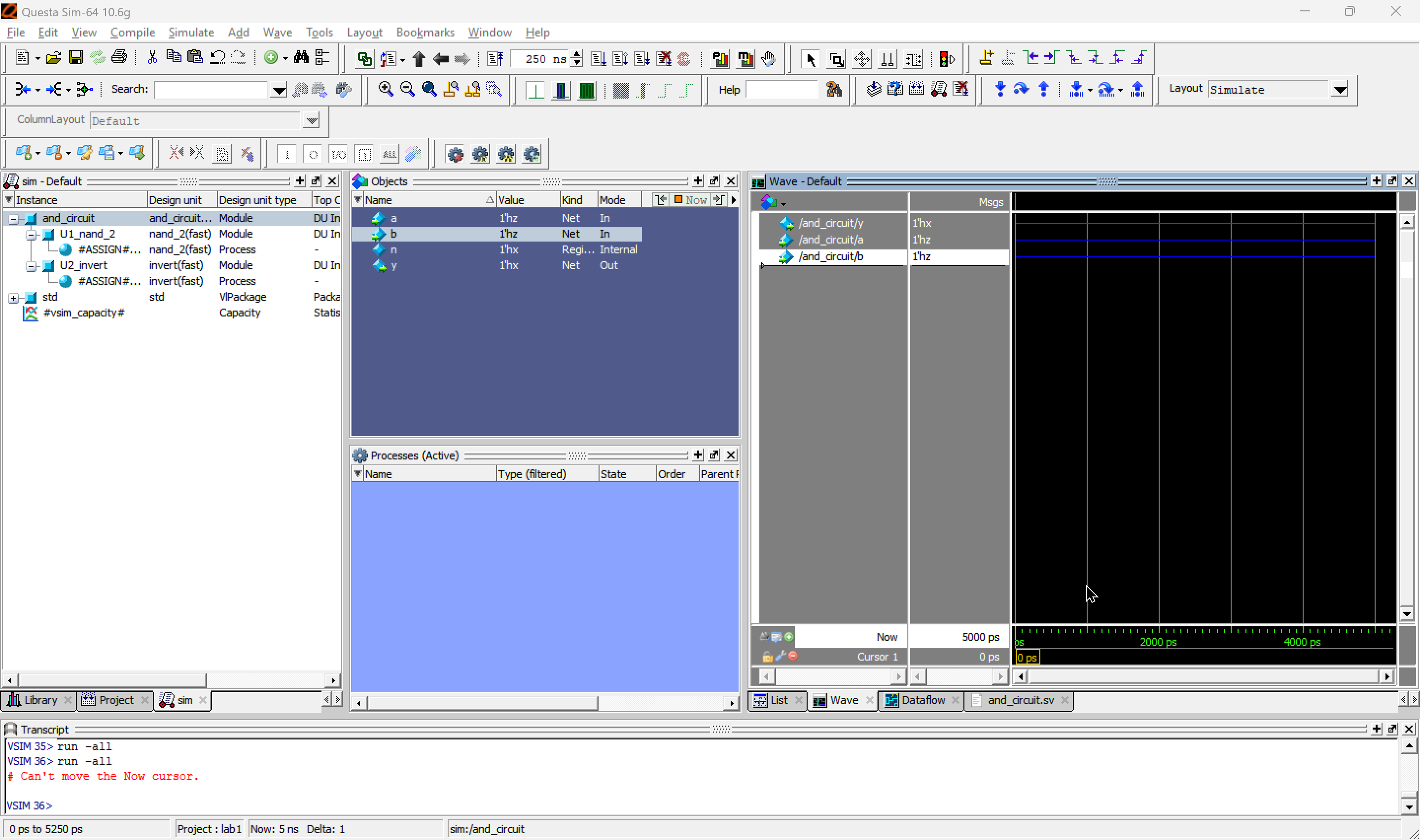
1B
#10
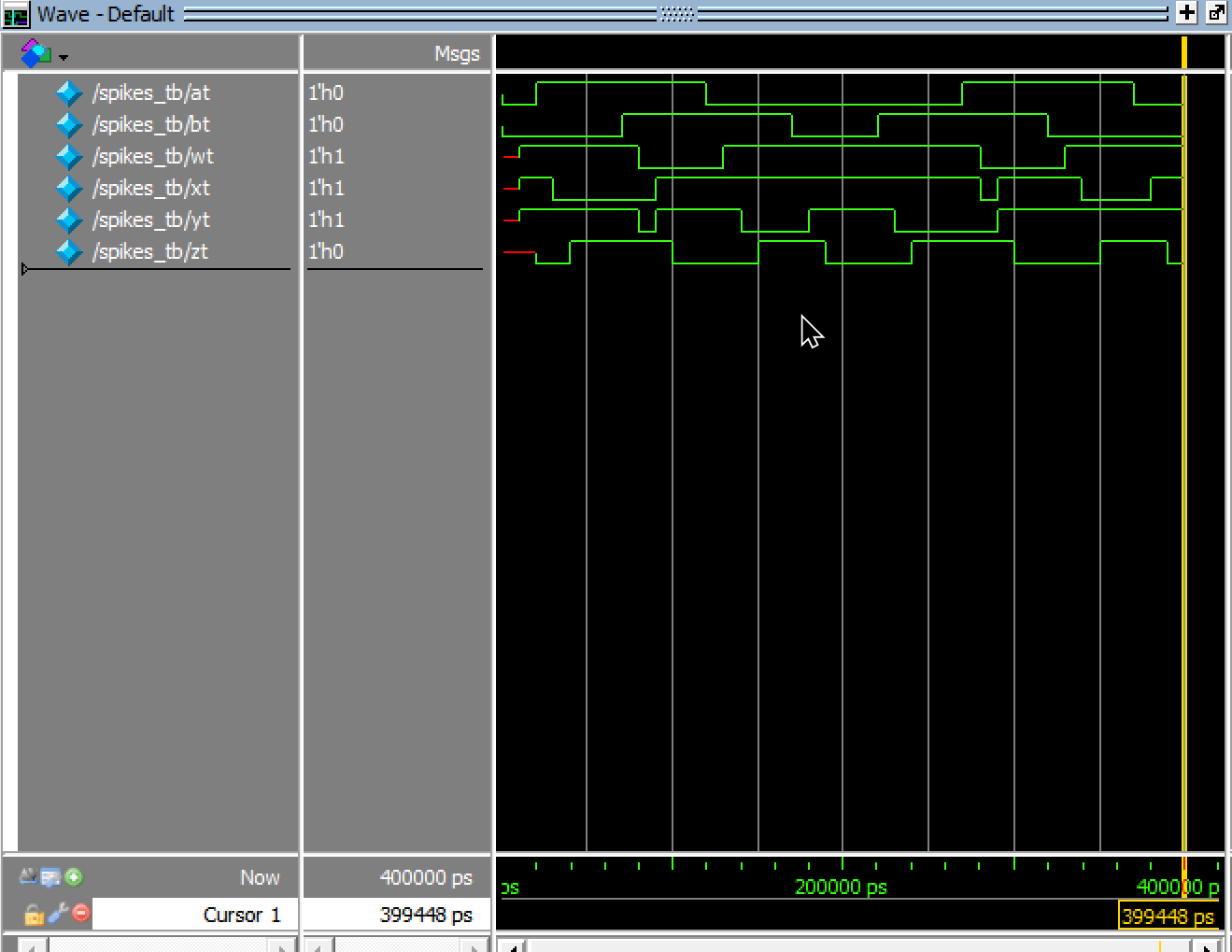
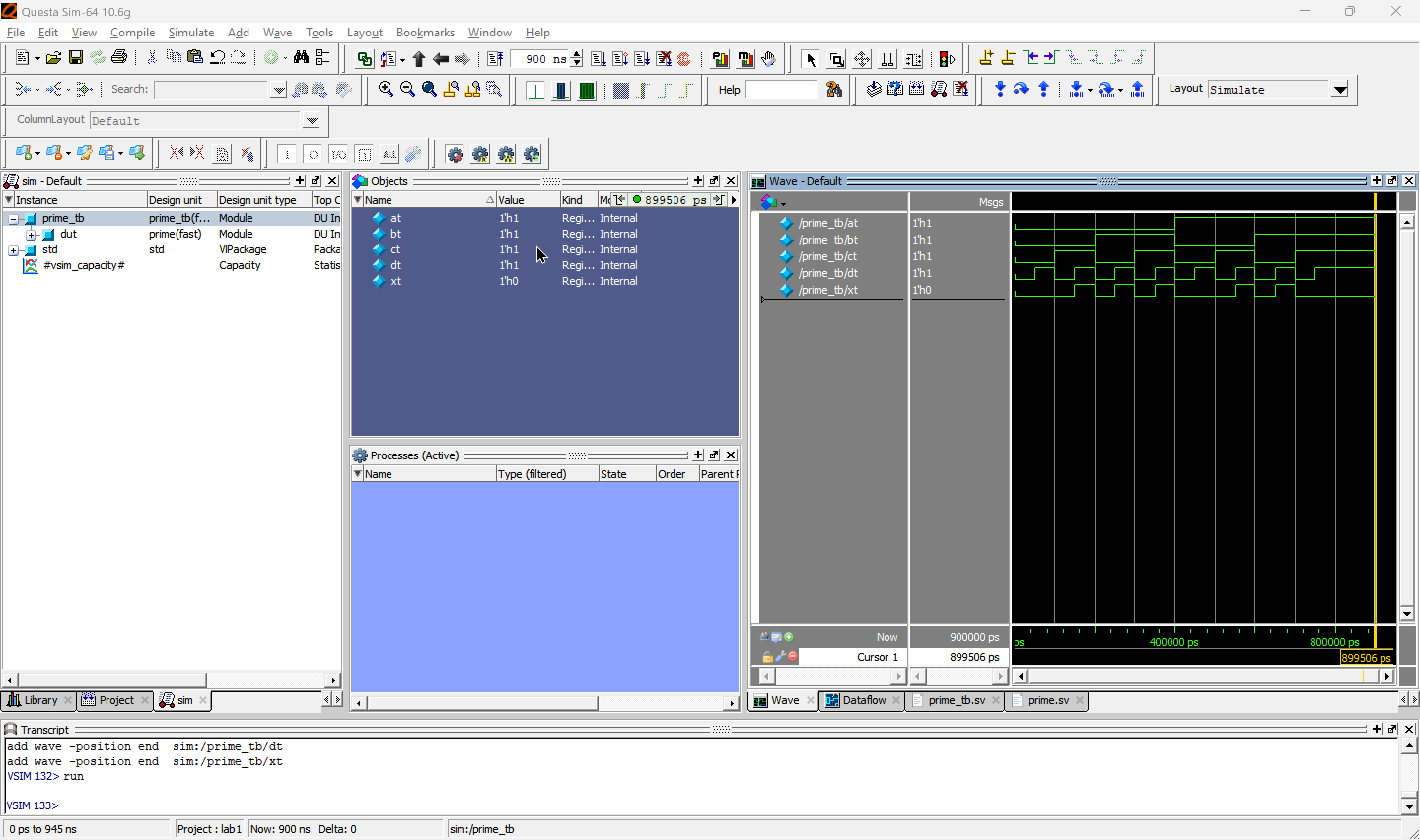
1C
{
"versionAtEmbed": "0.3.4",
"filepath": "lab/attachments/Ink/Drawing/2025.9.18 - 16.30pm.drawing",
"width": 500,
"aspectRatio": 1
}